Class 7: More pandas, Visualizations, xarray and Modeling

More pandas!

Working with String DataFrames

Pandas’ Series instances with a dtype of object or string expose a str attribute that enables vectorized string operations. These can come in tremendously handy, particularly when cleaning the data and performing aggregations on manually submitted fields.

For an in depth introduction to working with text data in pandas, see the relevant section in the documentation site.

Let’s imagine having the misfortune of reading some CSV data and finding the following headers:

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

messy_strings = [
    'Id___name', 'AGE', ' DomHand ', np.nan, 'qid    score1', 'score2', 3,
    ' COLOR_ SHAPe   _size', 'origin_residence immigration'
]
s = pd.Series(messy_strings, dtype="string", name="Messy Strings")
s

0                       Id___name
1                             AGE
2                        DomHand 
3                            <NA>
4                   qid    score1
5                          score2
6                               3
7            COLOR_ SHAPe   _size
8    origin_residence immigration
Name: Messy Strings, dtype: string

To try and parse something more reasonable, we might first want to remove all unnecessary whitespace and underscores. One way to achieve that would be:

s_1 = s.str.strip().str.replace("[_\s]+", " ", regex=True).str.lower()
s_1

0                         id name
1                             age
2                         domhand
3                            <NA>
4                      qid score1
5                          score2
6                               3
7                color shape size
8    origin residence immigration
Name: Messy Strings, dtype: string

Let’s break this down:

• strip() removed all whitespace from the beginning and end of the string.

• We used a regular expression to replace all one or more (+) occurrences of whitespace (\s) and underscores with single spaces.

• We converted all characters to lowercase.

Next, we’ll split() strings separated by whitespace and extract an array of the values:

s_2 = s_1.str.split(expand=True)
print(f"DataFrame:\n{s_2}")

s_3 = s_2.to_numpy().flatten()
print(f"\nArray:\n{s_3}")

DataFrame:
         0          1            2
0       id       name         <NA>
1      age       <NA>         <NA>
2  domhand       <NA>         <NA>
3     <NA>       <NA>         <NA>
4      qid     score1         <NA>
5   score2       <NA>         <NA>
6        3       <NA>         <NA>
7    color      shape         size
8   origin  residence  immigration

Array:
['id' 'name' <NA> 'age' <NA> <NA> 'domhand' <NA> <NA> <NA> <NA> <NA> 'qid'
 'score1' <NA> 'score2' <NA> <NA> '3' <NA> <NA> 'color' 'shape' 'size'
 'origin' 'residence' 'immigration']

Finally, we can get rid of the <NA> values:

column_names = s_3[~pd.isnull(s_3)]
column_names

array(['id', 'name', 'age', 'domhand', 'qid', 'score1', 'score2', '3',
       'color', 'shape', 'size', 'origin', 'residence', 'immigration'],
      dtype=object)

DataFrame String Operations Exercise

• Generate a 1000x1 shapedpd.DataFrame filled with 3-letter strings. Use the string module’s ascii_lowercase attribute and numpy’s random module.

Solution

import string
import numpy as np
import pandas as pd

letters = list(string.ascii_lowercase)
n_strings = 1000
string_length = 3 
string_generator = ("".join(np.random.choice(letters, string_length))
                    for _ in range(n_strings))
df = pd.DataFrame(string_generator, columns=["Letters"])

• Add a column indicating if the string in this row has a z in its 2nd character.

Solution

target_char = "z"
target_index = 1
df["z!"] = df["Letters"].str.find(target_char) == target_index

• Add a third column containing the capitalized and reversed versions of the original strings.

Solution

df["REVERSED"] = df["Letters"].str.upper().apply(lambda s: s[::-1])

Concatenation and Merging

Similarly to NumPy arrays, Series and DataFrame objects can be concatenated as well. However, having indices can often make this operation somewhat less trivial.

For an in depth introduction to merging, joining, concatentation, and comparison in pandas, see the relevant section in the documentation site.

ser1 = pd.Series(['a', 'b', 'c'], index=[1, 2, 3])
ser2 = pd.Series(['d', 'e', 'f'], index=[4, 5, 6])
pd.concat([ser1, ser2])  # row-wise (axis=0) by default

1    a
2    b
3    c
4    d
5    e
6    f
dtype: object

Let’s do the same with dataframes:

df1 = pd.DataFrame([['a', 'A'], ['b', 'B']], columns=['let', 'LET'], index=[0, 1])
df2 = pd.DataFrame([['c', 'C'], ['d', 'D']], columns=['let', 'LET'], index=[2, 3])
pd.concat([df1, df2])  # again, along the first axis

	let	LET
0	a	A
1	b	B
2	c	C
3	d	D

This time, let’s complicate things a bit, and introduce different column names:

df1 = pd.DataFrame([['a', 'A'], ['b', 'B']], columns=['let1', 'LET1'], index=[0, 1])
df2 = pd.DataFrame([['c', 'C'], ['d', 'D']], columns=['let2', 'LET2'], index=[2, 3])
pd.concat([df1, df2])  # pandas can't make the column index compatible, so it resorts to columnar concat

	let1	LET1	let2	LET2
0	a	A	NaN	NaN
1	b	B	NaN	NaN
2	NaN	NaN	c	C
3	NaN	NaN	d	D

The same result would be achieved by:

pd.concat([df1, df2], axis=1)

	let1	LET1	let2	LET2
0	a	A	NaN	NaN
1	b	B	NaN	NaN
2	NaN	NaN	c	C
3	NaN	NaN	d	D

But what happens if introduce overlapping indices?

df1 = pd.DataFrame([['a', 'A'], ['b', 'B']], columns=['let', 'LET'], index=[0, 1])
df2 = pd.DataFrame([['c', 'C'], ['d', 'D']], columns=['let', 'LET'], index=[0, 2])
pd.concat([df1, df2])

	let	LET
0	a	A
1	b	B
0	c	C
2	d	D

Nothing, really! While not recommended in practice, pandas won’t judge you.

If, however, we wish to keep the integrity of the indices, we can use the verify_integrity keyword:

df1 = pd.DataFrame([['a', 'A'], ['b', 'B']], columns=['let', 'LET'], index=[0, 1])
df2 = pd.DataFrame([['c', 'C'], ['d', 'D']], columns=['let', 'LET'], index=[0, 2])
pd.concat([df1, df2], verify_integrity=True)

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
Cell In[10], line 3
      1 df1 = pd.DataFrame([['a', 'A'], ['b', 'B']], columns=['let', 'LET'], index=[0, 1])
      2 df2 = pd.DataFrame([['c', 'C'], ['d', 'D']], columns=['let', 'LET'], index=[0, 2])
----> 3 pd.concat([df1, df2], verify_integrity=True)

File /opt/hostedtoolcache/Python/3.10.14/x64/lib/python3.10/site-packages/pandas/core/reshape/concat.py:395, in concat(objs, axis, join, ignore_index, keys, levels, names, verify_integrity, sort, copy)
    380     copy = False
    382 op = _Concatenator(
    383     objs,
    384     axis=axis,
   (...)
    392     sort=sort,
    393 )
--> 395 return op.get_result()

File /opt/hostedtoolcache/Python/3.10.14/x64/lib/python3.10/site-packages/pandas/core/reshape/concat.py:671, in _Concatenator.get_result(self)
    669 for obj in self.objs:
    670     indexers = {}
--> 671     for ax, new_labels in enumerate(self.new_axes):
    672         # ::-1 to convert BlockManager ax to DataFrame ax
    673         if ax == self.bm_axis:
    674             # Suppress reindexing on concat axis
    675             continue

File properties.pyx:36, in pandas._libs.properties.CachedProperty.__get__()

File /opt/hostedtoolcache/Python/3.10.14/x64/lib/python3.10/site-packages/pandas/core/reshape/concat.py:702, in _Concatenator.new_axes(self)
    699 @cache_readonly
    700 def new_axes(self) -> list[Index]:
    701     ndim = self._get_result_dim()
--> 702     return [
    703         self._get_concat_axis if i == self.bm_axis else self._get_comb_axis(i)
    704         for i in range(ndim)
    705     ]

File /opt/hostedtoolcache/Python/3.10.14/x64/lib/python3.10/site-packages/pandas/core/reshape/concat.py:703, in <listcomp>(.0)
    699 @cache_readonly
    700 def new_axes(self) -> list[Index]:
    701     ndim = self._get_result_dim()
    702     return [
--> 703         self._get_concat_axis if i == self.bm_axis else self._get_comb_axis(i)
    704         for i in range(ndim)
    705     ]

File properties.pyx:36, in pandas._libs.properties.CachedProperty.__get__()

File /opt/hostedtoolcache/Python/3.10.14/x64/lib/python3.10/site-packages/pandas/core/reshape/concat.py:766, in _Concatenator._get_concat_axis(self)
    761 else:
    762     concat_axis = _make_concat_multiindex(
    763         indexes, self.keys, self.levels, self.names
    764     )
--> 766 self._maybe_check_integrity(concat_axis)
    768 return concat_axis

File /opt/hostedtoolcache/Python/3.10.14/x64/lib/python3.10/site-packages/pandas/core/reshape/concat.py:774, in _Concatenator._maybe_check_integrity(self, concat_index)
    772 if not concat_index.is_unique:
    773     overlap = concat_index[concat_index.duplicated()].unique()
--> 774     raise ValueError(f"Indexes have overlapping values: {overlap}")

ValueError: Indexes have overlapping values: Index([0], dtype='int64')

If we don’t care about the indices, we can just ignore them:

pd.concat([df1, df2], ignore_index=True)  # resets the index

	let	LET
0	a	A
1	b	B
2	c	C
3	d	D

We can also create a new MultiIndex if that happens to makes more sense:

pd.concat([df1, df2], keys=['df1', 'df2'])  # "remembers" the origin of the data, super useful!

		let	LET
df1	0	a	A
	1	b	B
df2	0	c	C
	2	d	D

A common real world example of concatenation happens when joining two datasets sampled at different times. For example, if we conducted in day 1 measurements at times 8:00, 10:00, 14:00 and 16:00, but during day 2 we were a bit dizzy, and conducted the measurements at 8:00, 10:00, 13:00 and 16:30. On top of that, we recorded another parameter that we forget to measure at day 1.

The default concatenation behavior of pandas keeps all the data. In database terms (SQL people rejoice!) it’s called an “outer join”:

# Prepare mock data
day_1_times = pd.to_datetime(['08:00', '10:00', '14:00', '16:00'],
                             format='%H:%M').time
day_2_times = pd.to_datetime(['08:00', '10:00', '13:00', '16:30'],
                             format='%H:%M').time

day_1_data = {
    "temperature": [36.6, 36.7, 37.0, 36.8],
    "humidity": [30., 31., 30.4, 30.4]
}
day_2_data = {
    "temperature": [35.9, 36.1, 36.5, 36.2],
    "humidity": [32.2, 34.2, 30.9, 32.6],
    "light": [200, 130, 240, 210]
}

df_1 = pd.DataFrame(day_1_data, index=day_1_times)
df_2 = pd.DataFrame(day_2_data, index=day_2_times)

df_1

	temperature	humidity
08:00:00	36.6	30.0
10:00:00	36.7	31.0
14:00:00	37.0	30.4
16:00:00	36.8	30.4

Note

Note how pd.to_datetime() returns a DatetimeIndex object which exposes a time property, allowing us to easily remove the “date” part of the returned “datetime”, considering it is not represented in our mock data.

df_2

	temperature	humidity	light
08:00:00	35.9	32.2	200
10:00:00	36.1	34.2	130
13:00:00	36.5	30.9	240
16:30:00	36.2	32.6	210

# Outer join
pd.concat([df_1, df_2], join='outer')  # outer join is the default behavior  

	temperature	humidity	light
08:00:00	36.6	30.0	NaN
10:00:00	36.7	31.0	NaN
14:00:00	37.0	30.4	NaN
16:00:00	36.8	30.4	NaN
08:00:00	35.9	32.2	200.0
10:00:00	36.1	34.2	130.0
13:00:00	36.5	30.9	240.0
16:30:00	36.2	32.6	210.0

To take the intersection of the columns we have to use inner join. The intersection is all the columns that are common in all datasets.

# Inner join - the excess data column was dropped (index is still not unique)
pd.concat([df_1, df_2], join='inner')

	temperature	humidity
08:00:00	36.6	30.0
10:00:00	36.7	31.0
14:00:00	37.0	30.4
16:00:00	36.8	30.4
08:00:00	35.9	32.2
10:00:00	36.1	34.2
13:00:00	36.5	30.9
16:30:00	36.2	32.6

One can also specify the exact columns that should be the result of the join operation using the columns keyword. All in all, this basic functionality is easy to understand and allows for high flexibility.

Finally, joining on the columns will require the indices to be unique:

pd.concat([df_1, df_2], join='inner', axis='columns')

	temperature	humidity	temperature	humidity	light
08:00:00	36.6	30.0	35.9	32.2	200
10:00:00	36.7	31.0	36.1	34.2	130

This doesn’t look so good. The columns are a mess and we’re barely left with any data.

Our best option using pd.concat() might be something like:

df_concat = pd.concat([df_1, df_2], keys=["Day 1", "Day 2"])
df_concat

		temperature	humidity	light
Day 1	08:00:00	36.6	30.0	NaN
	10:00:00	36.7	31.0	NaN
	14:00:00	37.0	30.4	NaN
	16:00:00	36.8	30.4	NaN
Day 2	08:00:00	35.9	32.2	200.0
	10:00:00	36.1	34.2	130.0
	13:00:00	36.5	30.9	240.0
	16:30:00	36.2	32.6	210.0

Or maybe an unstacked version:

df_concat.unstack(0)

	temperature		humidity		light
	Day 1	Day 2	Day 1	Day 2	Day 1	Day 2
08:00:00	36.6	35.9	30.0	32.2	NaN	200.0
10:00:00	36.7	36.1	31.0	34.2	NaN	130.0
13:00:00	NaN	36.5	NaN	30.9	NaN	240.0
14:00:00	37.0	NaN	30.4	NaN	NaN	NaN
16:00:00	36.8	NaN	30.4	NaN	NaN	NaN
16:30:00	NaN	36.2	NaN	32.6	NaN	210.0

We could also use pd.merge():

pd.merge(df_1,
         df_2,
         how="outer",           # Keep all indices (rather than just the intersection)
         left_index=True,       # Use left index
         right_index=True,      # Use right index
         suffixes=("_1", "_2")) # Suffixes to use for overlapping columns

	temperature_1	humidity_1	temperature_2	humidity_2	light
08:00:00	36.6	30.0	35.9	32.2	200.0
10:00:00	36.7	31.0	36.1	34.2	130.0
13:00:00	NaN	NaN	36.5	30.9	240.0
14:00:00	37.0	30.4	NaN	NaN	NaN
16:00:00	36.8	30.4	NaN	NaN	NaN
16:30:00	NaN	NaN	36.2	32.6	210.0

The dataframe’s merge() method also enables easily combining columns from a different (but similarly indexed) dataframe:

mouse_id = [511, 512, 513, 514]
meas1 = [67, 66, 89, 92]
meas2 = [45, 45, 65, 61]

data_1 = {"ID": [500, 501, 502, 503], "Blood Volume": [100, 102, 99, 101]}
data_2 = {"ID": [500, 501, 502, 503], "Monocytes": [20, 19, 25, 21]}

df_1 = pd.DataFrame(data_1)
df_2 = pd.DataFrame(data_2)
df_1

	ID	Blood Volume
0	500	100
1	501	102
2	502	99
3	503	101

df_1.merge(df_2)  # merge identified that the only "key" connecting the two tables was the 'id' key

	ID	Blood Volume	Monocytes
0	500	100	20
1	501	102	19
2	502	99	25
3	503	101	21

Database-like operations are a very broad topic with advanced implementations in pandas.

Concatenation and Merging Exercise

• Create three dataframes with random values and shapes of (10, 2), (10, 1), (15, 3). Their index should be simple ordinal integers, and their column names should be different.

Solution

df_1 = pd.DataFrame(np.random.random((10, 2)), columns=['a', 'b'])
df_2 = pd.DataFrame(np.random.random((10, 1)), columns=['c'])
df_3 = pd.DataFrame(np.random.random((15, 3)), columns=['d', 'e', 'f'])

• Concatenate these dataframes over the second axis using pd.concat().

Solution

pd.concat([df_1, df_2, df_3], axis=1)

• Concatenate these dataframes over the second axis using pd.merge().

Solution

merge_kwargs = {"how": "outer", "left_index": True, "right_index": True}
pd.merge(pd.merge(df_1, df_2, **merge_kwargs), df_3, **merge_kwargs)

Grouping

Yet another SQL-like feature that pandas posses is the group-by operation, sometimes known as “split-apply-combine”.

# Mock data
subject = range(100, 200)
alive = np.random.choice([True, False], 100)
placebo = np.random.choice([True, False], 100)
measurement_1 = np.random.random(100)
measurement_2 = np.random.random(100)
data = {
    "Subject ID": subject,
    "Alive": alive,
    "Placebo": placebo,
    "Measurement 1": measurement_1,
    "Measurement 2": measurement_2
}
df = pd.DataFrame(data).set_index("Subject ID")
df

	Alive	Placebo	Measurement 1	Measurement 2
Subject ID
100	True	False	0.157922	0.448884
101	True	False	0.125746	0.289782
102	True	True	0.073862	0.759800
103	True	True	0.310033	0.954671
104	True	False	0.010180	0.752628
...	...	...	...	...
195	True	True	0.404811	0.664074
196	True	True	0.958644	0.294556
197	False	True	0.496004	0.003771
198	False	False	0.078334	0.696901
199	True	True	0.437749	0.495749

100 rows × 4 columns

The most sensible thing to do is to group by either the “Alive” or the “Placebo” columns (or both). This is the “split” part.

grouped = df.groupby('Alive')
grouped  # DataFrameGroupBy object - intermediate object ready to be evaluated

<pandas.core.groupby.generic.DataFrameGroupBy object at 0x7f82ad598340>

This intermediate object is an internal pandas representation which should allow it to run very fast computation the moment we want to actually know something about these groups. Assuming we want the mean of Measurement 1, as long as we won’t specifically write grouped.mean() pandas will do very little in terms of actual computation. It’s called “lazy evaluation”.

The intermediate object has some useful attributes:

grouped.groups

{False: [105, 107, 111, 112, 116, 117, 121, 122, 125, 127, 130, 132, 134, 135, 139, 140, 141, 142, 147, 148, 150, 152, 155, 156, 158, 159, 162, 163, 164, 167, 170, 173, 174, 175, 177, 179, 185, 186, 189, 192, 194, 197, 198], True: [100, 101, 102, 103, 104, 106, 108, 109, 110, 113, 114, 115, 118, 119, 120, 123, 124, 126, 128, 129, 131, 133, 136, 137, 138, 143, 144, 145, 146, 149, 151, 153, 154, 157, 160, 161, 165, 166, 168, 169, 171, 172, 176, 178, 180, 181, 182, 183, 184, 187, 188, 190, 191, 193, 195, 196, 199]}

len(grouped)  # True and False

2

If we wish to run some actual processing, we have to use an aggregation function:

grouped.sum()

	Placebo	Measurement 1	Measurement 2
Alive
False	16	20.662584	22.137268
True	32	25.915945	28.186884

grouped.mean()

	Placebo	Measurement 1	Measurement 2
Alive
False	0.372093	0.480525	0.514820
True	0.561404	0.454666	0.494507

grouped.size()

Alive
False    43
True     57
dtype: int64

If we just wish to see one of the groups, we can use get_group():

grouped.get_group(True).head()

	Alive	Placebo	Measurement 1	Measurement 2
Subject ID
100	True	False	0.157922	0.448884
101	True	False	0.125746	0.289782
102	True	True	0.073862	0.759800
103	True	True	0.310033	0.954671
104	True	False	0.010180	0.752628

We can also call several functions at once using the .agg attribute:

grouped.agg([np.mean, np.std]).drop("Placebo", axis=1)

/tmp/ipykernel_2080/773109026.py:1: FutureWarning: The provided callable <function mean at 0x7f82d4027e20> is currently using SeriesGroupBy.mean. In a future version of pandas, the provided callable will be used directly. To keep current behavior pass the string "mean" instead.
  grouped.agg([np.mean, np.std]).drop("Placebo", axis=1)
/tmp/ipykernel_2080/773109026.py:1: FutureWarning: The provided callable <function std at 0x7f82d4027f40> is currently using SeriesGroupBy.std. In a future version of pandas, the provided callable will be used directly. To keep current behavior pass the string "std" instead.
  grouped.agg([np.mean, np.std]).drop("Placebo", axis=1)

	Measurement 1		Measurement 2
	mean	std	mean	std
Alive
False	0.480525	0.259470	0.514820	0.255108
True	0.454666	0.277261	0.494507	0.293347

Grouping by multiple columns:

grouped2 = df.groupby(['Alive', 'Placebo'])
grouped2

<pandas.core.groupby.generic.DataFrameGroupBy object at 0x7f82ad599540>

grouped2.agg([np.sum, np.var])

/tmp/ipykernel_2080/557621468.py:1: FutureWarning: The provided callable <function sum at 0x7f82d4026ef0> is currently using SeriesGroupBy.sum. In a future version of pandas, the provided callable will be used directly. To keep current behavior pass the string "sum" instead.
  grouped2.agg([np.sum, np.var])
/tmp/ipykernel_2080/557621468.py:1: FutureWarning: The provided callable <function var at 0x7f82d40340d0> is currently using SeriesGroupBy.var. In a future version of pandas, the provided callable will be used directly. To keep current behavior pass the string "var" instead.
  grouped2.agg([np.sum, np.var])

		Measurement 1		Measurement 2
		sum	var	sum	var
Alive	Placebo
False	False	12.435154	0.075064	14.852352	0.057712
	True	8.227430	0.056471	7.284916	0.076174
True	False	10.851087	0.081401	11.740398	0.100569
	True	15.064858	0.075237	16.446486	0.076700

groupby() offers many more features, available here.

Grouping Exercise

• Create a dataframe with two columns, 10,000 entries in length. The first should be a random boolean column, and the second should be a sine wave from 0 to 20\(\pi\). This simulates measuring a parameter from two distinct groups.

Solution

boolean_groups = np.array([False, True])
n_subjects = 100
stop = 20 * np.pi
group_choice = np.random.choice(boolean_groups, n_subjects)
values = np.sin(np.linspace(start=0, stop=stop, num=n_subjects))
df = pd.DataFrame({'group': group_choice, 'value': values})

• Group the dataframe by your boolean column, creating a GroupBy object.

Solution

grouped = df.groupby("group")

• Plot the values of the grouped dataframe.

Solution

import matplotlib.pyplot as plt

fig, ax = plt.subplots(figsize=(15, 10))
grouped_plot = grouped.value.plot(ax=ax)

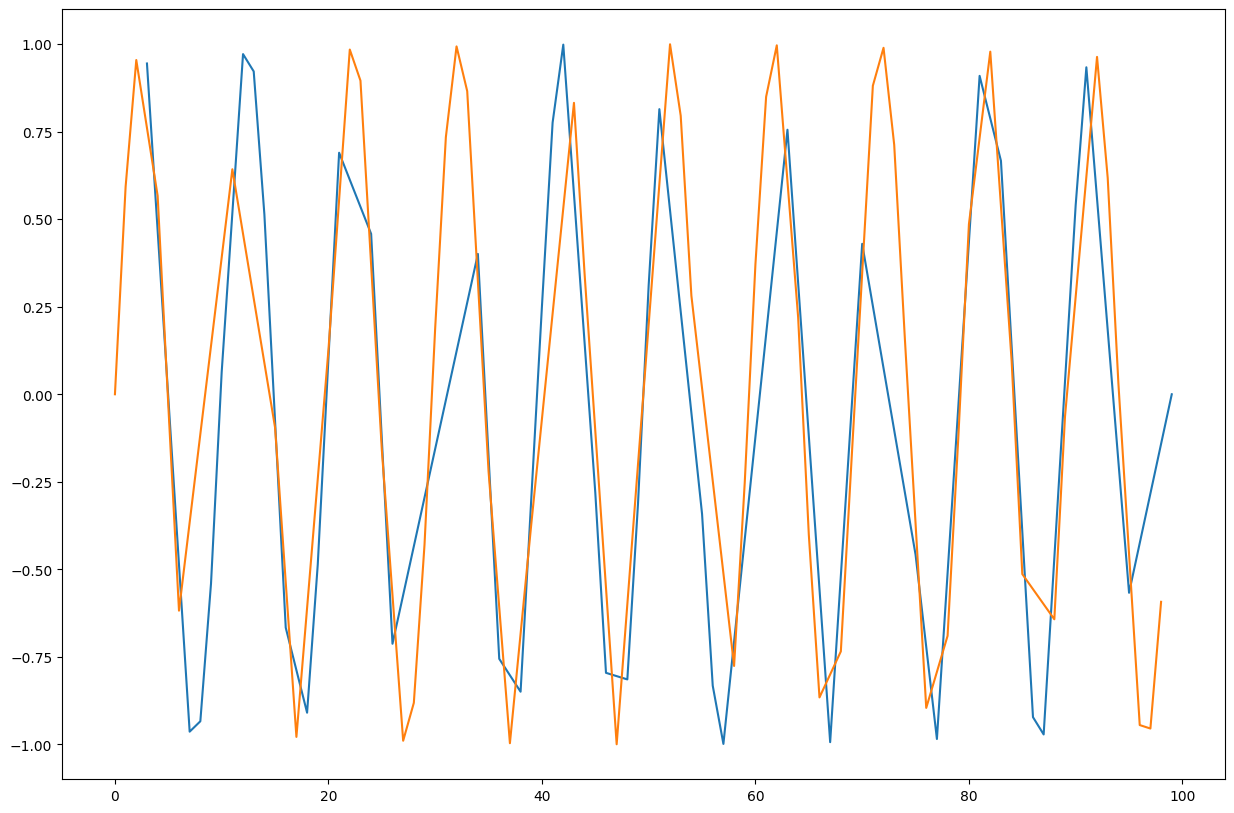
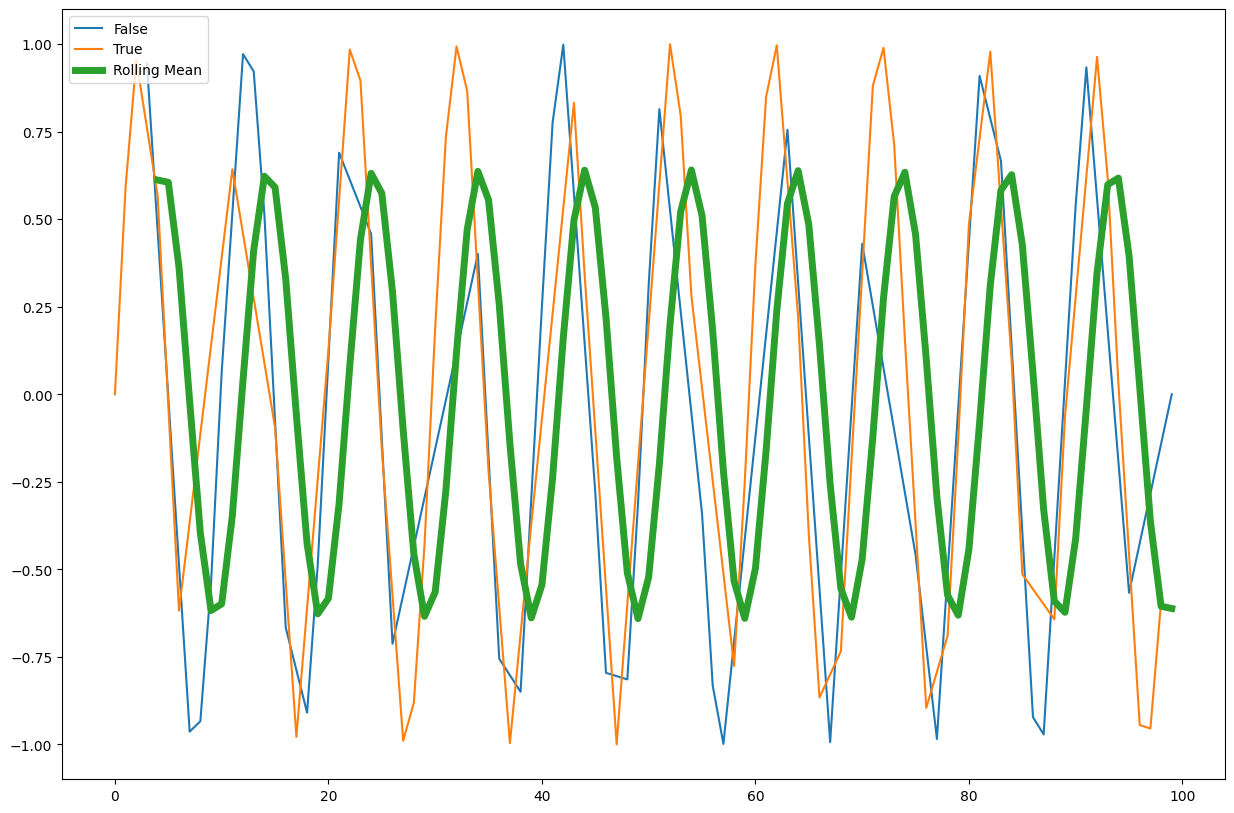
• Use the rolling() method to create a rolling average window of length 5 and overlay the result.

Solution

window_size = 5
rolling_mean = df.value.rolling(window=window_size).mean()
rolling_mean.plot(ax=ax, label="Rolling Mean", linewidth=5)
ax.legend(loc="upper left")

Other Pandas Features

Pandas has a TON of features and small implementation details that are there to make your life simpler. Features like IntervalIndex to index the data between two numbers instead of having a single label, for example, are very nice and ergonomic if you need them. Sparse DataFrames are also included, as well as many other computational tools, serialization capabilities, and more. If you need it - there’s a good chance it already exists as a method in the pandas jungle.

Data Visualization

As mentioned previously the visualization landscape in Python is rich, and is becoming richer by the day. Below, we’ll explore some of the options we have.

* We’ll assume that 2D data is accessed from a dataframe.

matplotlib

The built-in df.plot() method is a simple wrapper around pyplot from matplotlib, and as we’ve seen before it works quite well for many types of plots, as long as we wish to keep them all overlayed in some sort. Let’s look at examples taken straight from the visualization manual of pandas:

ts = pd.Series(np.random.randn(1000),
               index=pd.date_range('1/1/2000', periods=1000))
df = pd.DataFrame(np.random.randn(1000, 4),
                  index=ts.index,
                  columns=list('ABCD'))
df = df.cumsum()
df

	A	B	C	D
2000-01-01	-0.774807	2.927159	-2.413803	-0.411926
2000-01-02	-0.076706	4.266984	-2.720047	-0.113756
2000-01-03	-0.622351	4.767193	-3.311303	1.336423
2000-01-04	-1.406977	5.546904	-3.007523	0.416774
2000-01-05	-1.414479	6.909160	-3.151792	0.564072
...	...	...	...	...
2002-09-22	2.883340	53.362388	30.258674	21.362145
2002-09-23	4.630796	51.140830	30.231292	21.150303
2002-09-24	6.213404	51.074618	31.558736	23.333177
2002-09-25	6.943851	50.778649	31.910856	21.208530
2002-09-26	6.998486	51.523504	29.251967	22.685471

1000 rows × 4 columns

_ = df.plot()

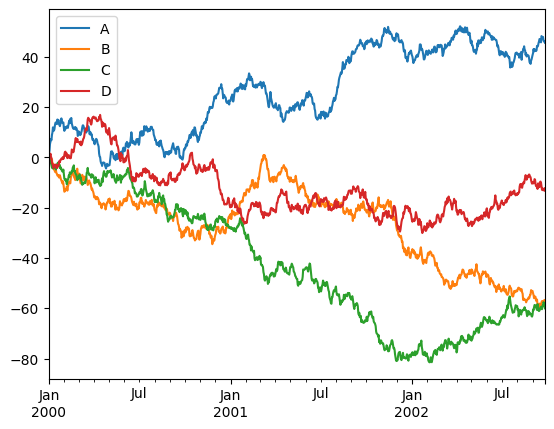
Nice to see we got a few things for “free”, like sane x-axis labels and the legend.

We can tell pandas which column corresponds to x, and which to y:

_ = df.plot(x='A', y='B')

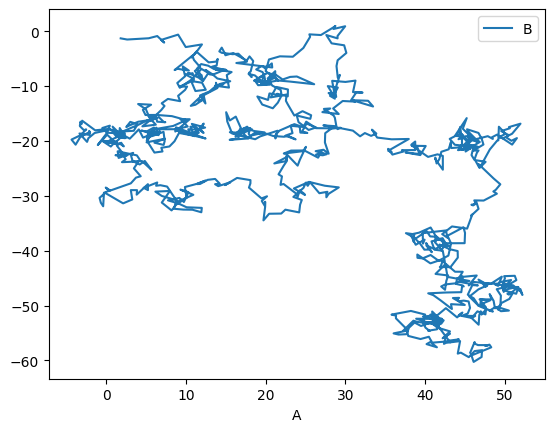
There are, of course, many possible types of plots that can be directly called from the pandas interface:

_ = df.iloc[:10, :].plot.bar()

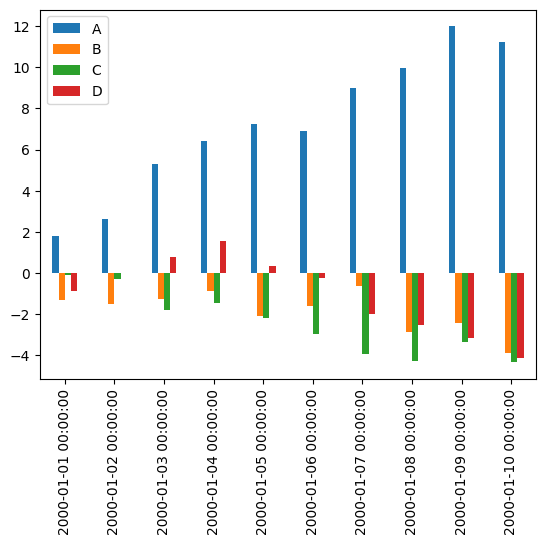
_ = df.plot.hist(alpha=0.5)

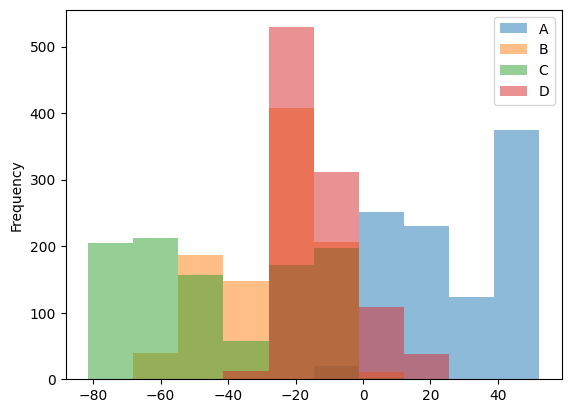
Histogramming each column separately can be done by calling the hist() method directly:

_ = df.hist()

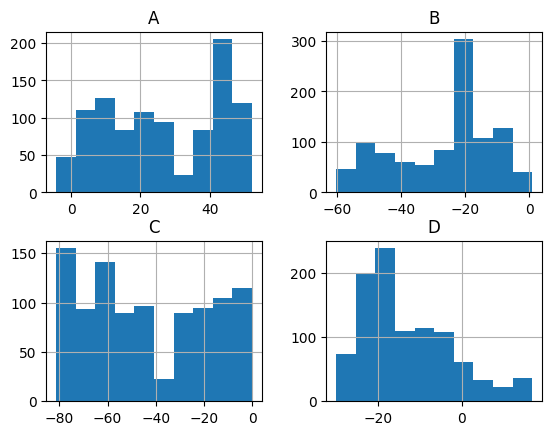
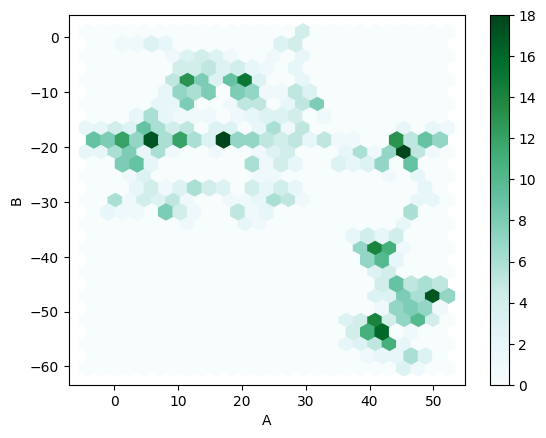
Lastly, a personal favorite:

_ = df.plot.hexbin(x='A', y='B', gridsize=25)

Altair

Matplotlib (and pandas’ interface to it) is the gold standard in the Python ecosystem - but there are other ecosystems as well. For example, vega-lite is a famous plotting library for the web and Javascript, and it uses a different grammar to define its plots. If you’re familiar with it you’ll be delighted to hear that Python’s altair provides bindings to it, and even if you’ve never heard of it it’s always nice to see that there are many other different ways to tell a computer how to draw stuff on the screen. Let’s look at a couple of examples:

import altair as alt

chart = alt.Chart(df)
chart.mark_point().encode(x='A', y='B')

In Altair you first create a chart object (a simple Chart above), and then you ask it to mark_point(), or mark_line(), to add that type of visualization to the chart. Then we specify the axis and other types of parameters (like color) and map (or encode) them to their corresponding column.

Let’s see how Altair works with other datatypes:

datetime_df = pd.DataFrame({'value': np.random.randn(100).cumsum()},
                           index=pd.date_range('2020', freq='D', periods=100))

datetime_df.head()

	value
2020-01-01	-1.053172
2020-01-02	-0.935523
2020-01-03	-1.169427
2020-01-04	0.060736
2020-01-05	0.610130

chart = alt.Chart(datetime_df.reset_index())
chart.mark_line().encode(x='index:T', y='value:Q')

Above we plot the datetime data by telling Altair that the column named “index” is of type T, i.e. Time, while the column “value” is of type Q for quantitative.

One of the great things about these charts is that they can easily be made to be interactive:

from vega_datasets import data  # ready-made DFs for easy visualization examples

cars = data.cars
cars()

	Name	Miles_per_Gallon	Cylinders	Displacement	Horsepower	Weight_in_lbs	Acceleration	Year	Origin
0	chevrolet chevelle malibu	18.0	8	307.0	130.0	3504	12.0	1970-01-01	USA
1	buick skylark 320	15.0	8	350.0	165.0	3693	11.5	1970-01-01	USA
2	plymouth satellite	18.0	8	318.0	150.0	3436	11.0	1970-01-01	USA
3	amc rebel sst	16.0	8	304.0	150.0	3433	12.0	1970-01-01	USA
4	ford torino	17.0	8	302.0	140.0	3449	10.5	1970-01-01	USA
...	...	...	...	...	...	...	...	...	...
401	ford mustang gl	27.0	4	140.0	86.0	2790	15.6	1982-01-01	USA
402	vw pickup	44.0	4	97.0	52.0	2130	24.6	1982-01-01	Europe
403	dodge rampage	32.0	4	135.0	84.0	2295	11.6	1982-01-01	USA
404	ford ranger	28.0	4	120.0	79.0	2625	18.6	1982-01-01	USA
405	chevy s-10	31.0	4	119.0	82.0	2720	19.4	1982-01-01	USA

406 rows × 9 columns

cars_url = data.cars.url
cars_url  # The data is online and in json format which is standard practice for altair-based workflows

'https://cdn.jsdelivr.net/npm/vega-datasets@v1.29.0/data/cars.json'

alt.Chart(cars_url).mark_point().encode(
    x='Miles_per_Gallon:Q',
    y='Horsepower:Q',
    color='Origin:N',  # N for nominal, i.e. discrete and unordered (just like colors)
)

brush = alt.selection_interval()  # selection of type 'interval'

alt.Chart(cars_url).mark_point().encode(
    x='Miles_per_Gallon:Q',
    y='Horsepower:Q',
    color='Origin:N',  # N for nominal, i.e.discrete and unordered (just like colors)
).add_selection(brush)

The selection looks good but doesn’t do anything. Let’s add functionality:

alt.Chart(cars_url).mark_point().encode(
    x='Miles_per_Gallon:Q',
    y='Horsepower:Q',
    color=alt.condition(brush, 'Origin:N', alt.value('lightgray'))
).add_selection(
    brush
)

Altair has a ton more visualization types, some of which are more easily generated than others, and some are easier to generate using Altair rather than Matplotlib.

Bokeh, Holoviews and pandas-bokeh

Bokeh is another visualization effort in the Python ecosystem, but this time it revolves around web-based plots. Bokeh can be used directly, but it also serves as a backend plotting device for more advanced plotting libraries, like Holoviews and pandas-bokeh. It’s also designed in mind with huge datasets that don’t fit in memory, which is something that other tools might have trouble visualizing.

import bokeh
from bokeh.io import output_notebook, show
from bokeh.plotting import figure as bkfig
output_notebook()

Loading BokehJS ...

bokeh_figure = bkfig(width=400, height=400)
x = [1, 2, 3, 4, 5]
y = [6, 7, 2, 4, 5]
bokeh_figure.circle(x,
                    y,
                    size=15,
                    line_color="navy",
                    fill_color="orange",
                    fill_alpha=0.5)

show(bokeh_figure)

BokehDeprecationWarning: 'circle() method with size value' was deprecated in Bokeh 3.4.0 and will be removed, use 'scatter(size=...) instead' instead.

We see how bokeh immediately outputs an interactive graph, i.e. an HTML document that will open in your browser (a couple of cells above we kindly asked bokeh to output its plots to the notebook instead). Bokeh can be used for many other types of plots, like:

datetime_df = datetime_df.reset_index()
datetime_df

	index	value
0	2020-01-01	-1.053172
1	2020-01-02	-0.935523
2	2020-01-03	-1.169427
3	2020-01-04	0.060736
4	2020-01-05	0.610130
...	...	...
95	2020-04-05	0.229688
96	2020-04-06	0.406019
97	2020-04-07	0.427744
98	2020-04-08	0.525765
99	2020-04-09	0.787080

100 rows × 2 columns

bokeh_figure_2 = bkfig(x_axis_type="datetime",
                       title="Value over Time",
                       height=350,
                       width=800)

bokeh_figure_2.xgrid.grid_line_color = None
bokeh_figure_2.ygrid.grid_line_alpha = 0.5
bokeh_figure_2.xaxis.axis_label = 'Time'
bokeh_figure_2.yaxis.axis_label = 'Value'

bokeh_figure_2.line(datetime_df.index, datetime_df.value)
show(bokeh_figure_2)

Let’s look at energy consumption, split by source (from the Pandas-Bokeh manual):

url = "https://raw.githubusercontent.com/PatrikHlobil/Pandas-Bokeh/master/docs/Testdata/energy/energy.csv"
df_energy = pd.read_csv(url, parse_dates=["Year"])
df_energy.head()

	Year	Oil	Gas	Coal	Nuclear Energy	Hydroelectricity	Other Renewable
0	1970-01-01	2291.5	826.7	1467.3	17.7	265.8	5.8
1	1971-01-01	2427.7	884.8	1459.2	24.9	276.4	6.3
2	1972-01-01	2613.9	933.7	1475.7	34.1	288.9	6.8
3	1973-01-01	2818.1	978.0	1519.6	45.9	292.5	7.3
4	1974-01-01	2777.3	1001.9	1520.9	59.6	321.1	7.7

Another Bokeh-based library is Holoviews. Its uniqueness stems from the way it handles DataFrames with multiple columns, and the way you add plots to each other. It’s very suitable for Jupyter notebook based plots:

import holoviews as hv
hv.extension("bokeh")

df_energy.head()

	Year	Oil	Gas	Coal	Nuclear Energy	Hydroelectricity	Other Renewable
0	1970-01-01	2291.5	826.7	1467.3	17.7	265.8	5.8
1	1971-01-01	2427.7	884.8	1459.2	24.9	276.4	6.3
2	1972-01-01	2613.9	933.7	1475.7	34.1	288.9	6.8
3	1973-01-01	2818.1	978.0	1519.6	45.9	292.5	7.3
4	1974-01-01	2777.3	1001.9	1520.9	59.6	321.1	7.7

scatter = hv.Scatter(df_energy, 'Oil', 'Gas')
scatter

scatter + hv.Curve(df_energy, 'Oil', 'Hydroelectricity')

def get_year_coal(df, year) -> int:
    return df.loc[df["Year"] == year, "Coal"]

items = {year: hv.Bars(get_year_coal(df_energy, year)) for year in df_energy["Year"]}
                       
hv.HoloMap(items, kdims=['Year'])

Holoviews really needs an entire class (or two) to go over its concepts, but once you get them you can create complicated visualizations which include a strong interactive component in a few lines of code.

Seaborn

A library which has really become a shining example of quick, efficient and clear plotting in the post-pandas era is seaborn. It combines many of the features of the previous libraries into a very concise API. Unlike a few of the previous libraries, however, it doesn’t use bokeh as its backend, but matplotlib, which means that the interactivity of the resulting plots isn’t as good. Be that as it may, it’s still a widely used library, and for good reasons.

In order to use seaborn to its full extent (and really all of the above libraries) we have to take a short detour and understand how to transform our data into a long-form format.

Long form (“tidy”) data

Tidy data was first defined in the R language (its “tidyverse” subset) as the preferred format for analysis and visualization. If you assume that the data you’re about to visualize is always in such a format, you can design plotting libraries that use these assumptions to cut the number of lines of code you have to write in order to see the final art. Tidy data migrated to the Pythonic data science ecosystem, and nowadays it’s the preferred data format in the pandas ecosystem as well. The way to construct a “tidy” table is to follow three simple rules:

1. Each variable forms a column.

2. Each observation forms a row.

3. Each type of observational unit forms a table.

In the paper defining tidy data, the following example is given - Assume we have the following data table:

name	treatment a	treatment b
John Smith	-	20.1
Jane Doe	15.1	13.2
Mary Johnson	22.8	27.5

Is this the “tidy” form? What are the variables and observations here? Well, we could’ve written this table in a different (‘transposed’) format:

treatment type	John Smith	Jane Doe	Mary Johnson
treat. a	-	15.1	22.8
treat. b	20.1	13.2	27.5

Is this “long form”?

In both cases, the answer is no. We have to move each observation into its own row, and in the above two tables two (or more) observations were placed in the same row. For example, Both observations concerning Mary Johnson (the measured value of treatment a and b) were located in the same row, which violates rule #2 of the “tidy” data rules. This is how the tidy version of the above tables look like:

name	treatment	measurement
John Doe	a	-
Jane Doe	a	15.1
Mary Johnson	a	22.8
John Doe	b	20.1
Jane Doe	b	13.2
Mary Johnson	b	27.5

Now each measurement has a single row, and the treatment column became an “index” of some sort. The only shortcoming of this approach is the fact that we now have more cells in the table. We had 9 in the previous two versions, but this one has 18. This is quite a jump, but if we’re smart about our data types (categorical data types) then the jump in memory usage wouldn’t become too hard.

As I wrote in the previous class, pandas has methods to transform data into its long form. You’ll usually need to use df.stack() or df.melt() to make it tidy. Let’s try to make our own data tidy:

df = pd.read_csv("pew_raw.csv")
df

	religion	10000	20000	30000	40000	50000	75000
0	Agnostic	27	34	60	81	76	137
1	Atheist	12	27	37	52	35	70
2	Buddhist	27	21	30	34	33	58
3	Catholic	418	617	732	670	638	1116
4	Dont know/refused	15	14	15	11	10	35
5	Evangelical Prot	575	869	1064	982	881	1486
6	Hindu	1	9	7	9	11	34
7	Historically Black Prot	228	244	236	238	197	223
8	Jehovahs Witness	20	27	24	24	21	30
9	Jewish	19	19	25	25	30	95

This is a table from the Pew Research Center on the relations between income (in USD) and religion. This dataset is not in a tidy format since the column headers contain information about specific observations (measurements). For example, the 27 agnostic individuals who donated less than $10k represent a measurement, and the 34 that donated $10k-20k represent another one, and so on.

To make it tidy we’ll use melt():

tidy_df = (pd.melt(df,
                  id_vars=["religion"],
                  var_name="income",
                  value_name="freq")
           .sort_values(by="religion")
           .reset_index(drop=True)
           .astype({'income': 'category', 'religion': 'category'}))

tidy_df

	religion	income	freq
0	Agnostic	10000	27
1	Agnostic	40000	81
2	Agnostic	50000	76
3	Agnostic	75000	137
4	Agnostic	20000	34
5	Agnostic	30000	60
6	Atheist	50000	35
7	Atheist	30000	37
8	Atheist	20000	27
9	Atheist	40000	52
10	Atheist	10000	12
11	Atheist	75000	70
12	Buddhist	50000	33
13	Buddhist	10000	27
14	Buddhist	20000	21
15	Buddhist	40000	34
16	Buddhist	75000	58
17	Buddhist	30000	30
18	Catholic	50000	638
19	Catholic	40000	670
20	Catholic	30000	732
21	Catholic	75000	1116
22	Catholic	20000	617
23	Catholic	10000	418
24	Dont know/refused	30000	15
25	Dont know/refused	50000	10
26	Dont know/refused	10000	15
27	Dont know/refused	75000	35
28	Dont know/refused	20000	14
29	Dont know/refused	40000	11
30	Evangelical Prot	30000	1064
31	Evangelical Prot	75000	1486
32	Evangelical Prot	20000	869
33	Evangelical Prot	10000	575
34	Evangelical Prot	50000	881
35	Evangelical Prot	40000	982
36	Hindu	75000	34
37	Hindu	30000	7
38	Hindu	50000	11
39	Hindu	20000	9
40	Hindu	40000	9
41	Hindu	10000	1
42	Historically Black Prot	50000	197
43	Historically Black Prot	40000	238
44	Historically Black Prot	75000	223
45	Historically Black Prot	30000	236
46	Historically Black Prot	20000	244
47	Historically Black Prot	10000	228
48	Jehovahs Witness	10000	20
49	Jehovahs Witness	40000	24
50	Jehovahs Witness	75000	30
51	Jehovahs Witness	50000	21
52	Jehovahs Witness	30000	24
53	Jehovahs Witness	20000	27
54	Jewish	30000	25
55	Jewish	40000	25
56	Jewish	20000	19
57	Jewish	10000	19
58	Jewish	50000	30
59	Jewish	75000	95

The first argument to melt is the column name that will be used as the “identifier variable”, i.e. will be repeated as necessary to be used as an “index” of some sorts. var_name is the new name of the column we made from the values in the old columns, and value_name is the name of the column that contains the actual values in the cells from before.

After the melting I sorted the dataframe to make it look prettier (all agnostics in row, etc.) and threw away the old and irrelevant index. Finally I converted the “religion” and “income” columns to a categorical data type, which saves memory and better conveys their true meaning.

Now, once we have this long form data, we can put seaborn to the test.

import seaborn as sns

income_barplot = sns.barplot(data=tidy_df, x='income', y='freq', hue='religion')

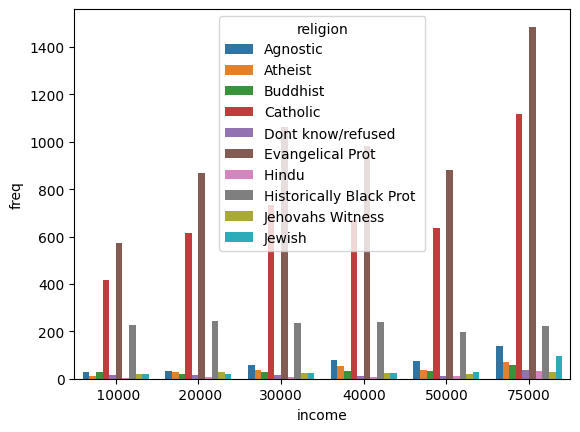
To fix the legend location:

income_barplot = sns.barplot(data=tidy_df, x='income', y='freq', hue='religion')
_ = income_barplot.legend(bbox_to_anchor=(1, 1))

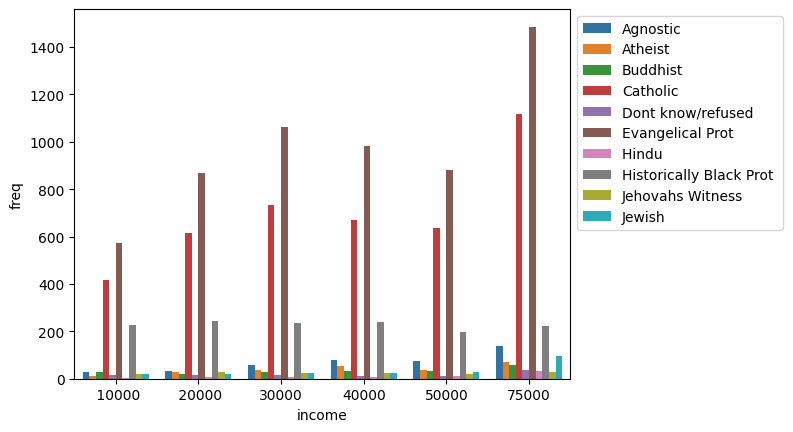
Each seaborn visualization functions has a “data” keyword to which you pass your dataframe, and then a few other with which you specify the relations of the columns to one another. Look how simple it was to receive this beautiful bar chart.

income_catplot = sns.catplot(data=tidy_df, x="religion", y="freq", hue="income", aspect=2)
_ = plt.xticks(rotation=45)

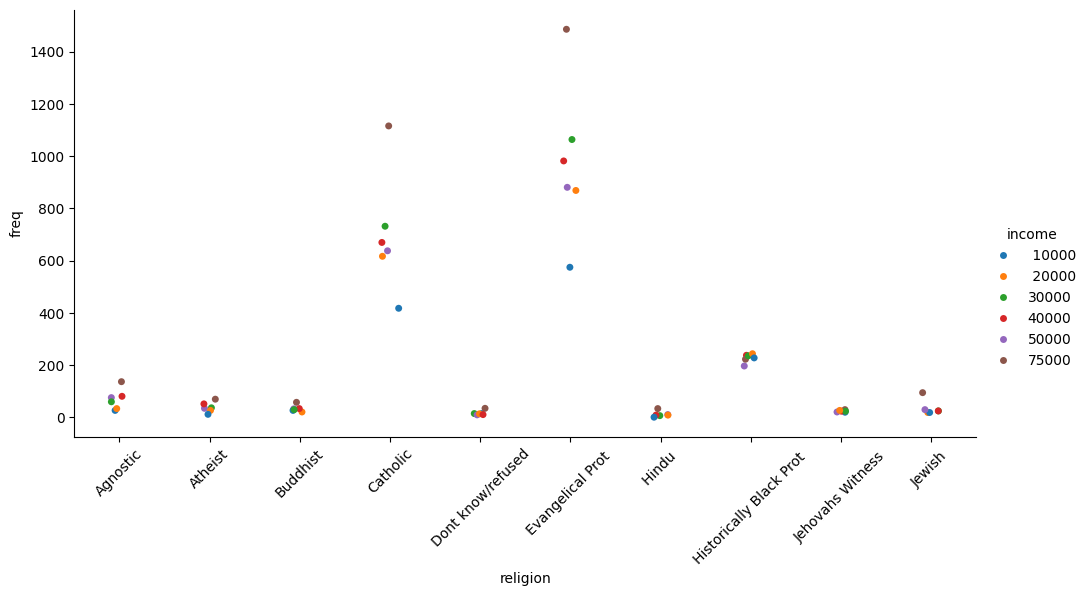
Seaborn also takes care of faceting the data for us:

_ = sns.catplot(data=tidy_df, x="religion", y="freq", hue="income", col="income")

Figure is a bit small? We can use matplotlib to change it:

_, ax = plt.subplots(figsize=(25, 8))
_ = sns.stripplot(data=tidy_df, x="religion", y="freq", hue="income", ax=ax)

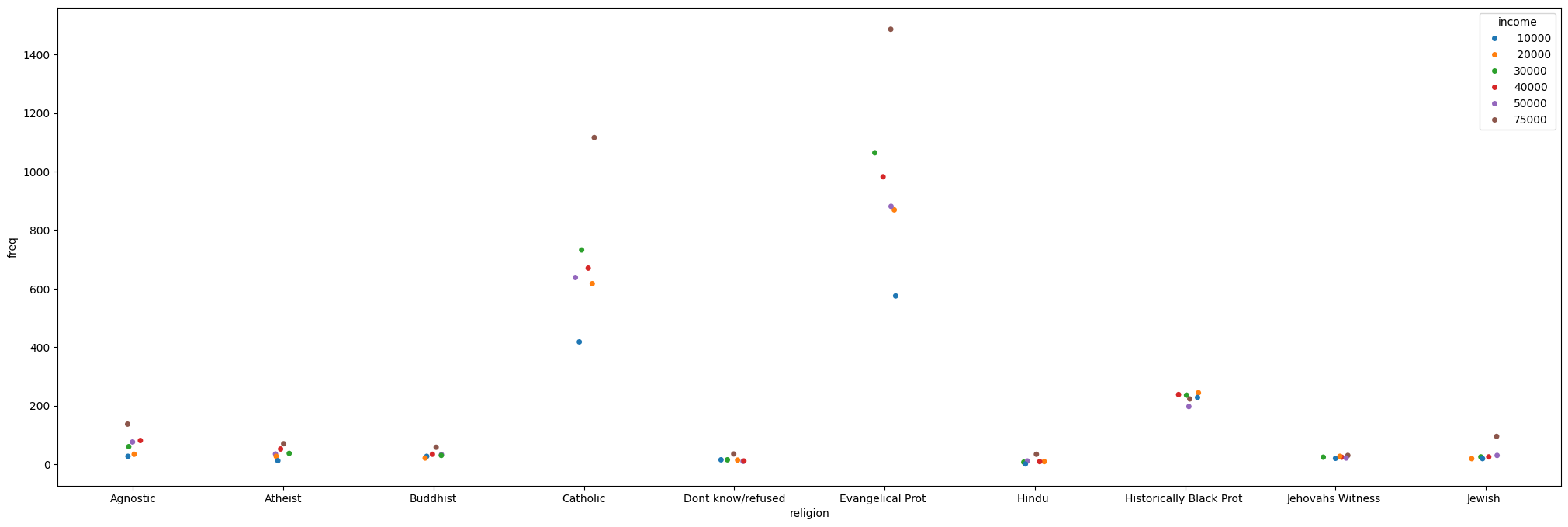
Simpler data can also be visualized, no need for categorical variables:

simple_df = pd.DataFrame(np.random.random((1000, 4)), columns=list('abcd'))
simple_df

	a	b	c	d
0	0.438704	0.582401	0.319232	0.631421
1	0.904376	0.597247	0.486666	0.237135
2	0.243257	0.679277	0.214461	0.748950
3	0.367532	0.437253	0.519017	0.786271
4	0.080251	0.789424	0.656212	0.256607
...	...	...	...	...
995	0.525036	0.539358	0.907704	0.884078
996	0.895862	0.648718	0.012188	0.615759
997	0.691116	0.549880	0.085899	0.939616
998	0.044483	0.869355	0.112515	0.667402
999	0.515885	0.668783	0.563677	0.026543

1000 rows × 4 columns

_ = sns.jointplot(data=simple_df, x='a', y='b', kind='kde')

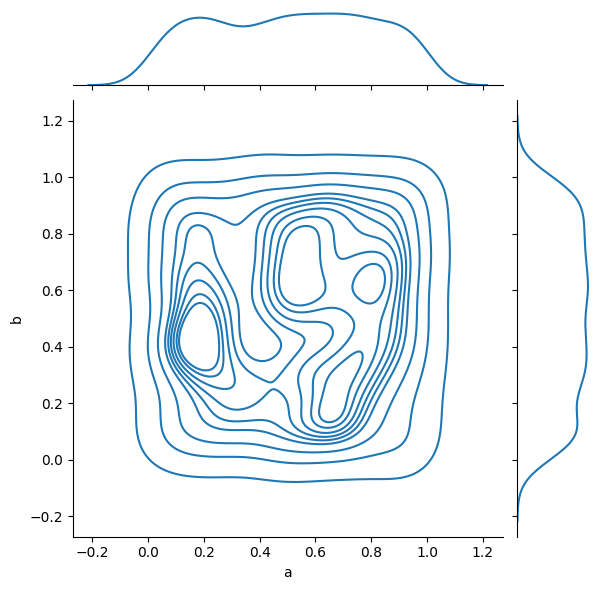
And complex relations can also be visualized:

_ = sns.pairplot(data=simple_df)

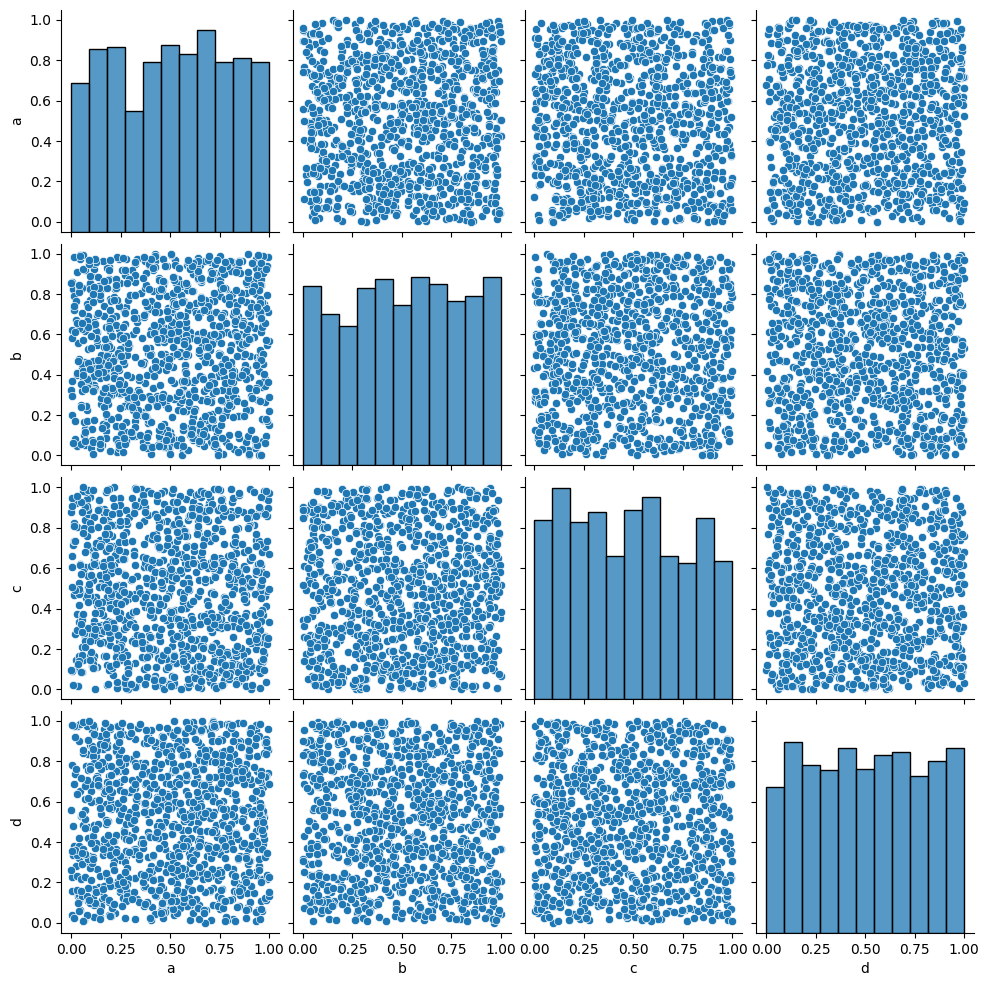
Seaborn should probably be your go-to choice when all you need is a 2D graph.

Higher Dimensionality: xarray

Pandas is amazing, but has its limits. A DataFrame can be a multi-dimensional container when using a MultiIndex, but it’s limited to a subset of uses in which another layer of indexing makes sense.

In many occasions, however, our data is truly high-dimensional. A simple case could be electro-physiological recordings, or calcium traces. In these cases we have several indices (some can be categorical), like “Sex”, “AnimalID”, “Date”, “TypeOfExperiment” and perhaps a few more. But the data itself is a vector of numbers representing voltage or fluorescence. Having this data in a dataframe seems a bit “off”, what are the columns on this dataframe? Is each column a voltage measurement? Or if each column is a measurement, how do you deal with the indices? We can use nested columns (MultiIndex the columns), but it’s not a very modular approach.

This is a classic example where pandas’ dataframes “fail”, and indeed pandas used to have a higher-dimensionality container named Panel. However, in late 2016 pandas developers deprecated it, publicly announcing that they intend to drop support for Panels sometime in the future, and whoever needs a higher-dimensionality container should use xarray.

xarray is a labeled n-dimensional array. Just like a DataFrame is a labeled 2D array, i.e. with names to its axes rather than numbers, in xarray each dimension has a name (time, temp, voltage) and its indices (“coordinates”) can also have labels (like a timestamp, for example). In addition, each xarray object also has metadata attached to it, in which we can write details that do not fit a columnar structure (experimenter name, hardware and software used for acquisition, etc.).

DataArray

import numpy as np
import xarray as xr

da = xr.DataArray(np.random.random((10, 2)))
da

<xarray.DataArray (dim_0: 10, dim_1: 2)> Size: 160B
array([[0.76995898, 0.03126021],
       [0.76400887, 0.64126327],
       [0.20350213, 0.4635834 ],
       [0.86582915, 0.20263217],
       [0.42274996, 0.67091027],
       [0.75127929, 0.01813313],
       [0.81732532, 0.40918105],
       [0.08500303, 0.0341819 ],
       [0.78106711, 0.69666425],
       [0.92082179, 0.53160548]])
Dimensions without coordinates: dim_0, dim_1

xarray.DataArray

• dim_0: 10
• dim_1: 2

• 0.77 0.03126 0.764 0.6413 0.2035 ... 0.7811 0.6967 0.9208 0.5316

  array([[0.76995898, 0.03126021],
         [0.76400887, 0.64126327],
         [0.20350213, 0.4635834 ],
         [0.86582915, 0.20263217],
         [0.42274996, 0.67091027],
         [0.75127929, 0.01813313],
         [0.81732532, 0.40918105],
         [0.08500303, 0.0341819 ],
         [0.78106711, 0.69666425],
         [0.92082179, 0.53160548]])

• Coordinates: (0)
• Indexes: (0)
• Attributes: (0)

The basic building block of xarray is a DataArray, an n-dimensional counter part of a pandas’ Series. It has two dimensions, just like the numpy array that its based upon. We didn’t specify names for these dimensions, so currently they’re called dim_0 and dim_1. We also didn’t specify coordinates (indices), so the printout doesn’t report of any coordinates for the data.

da.values  # just like pandas

array([[0.76995898, 0.03126021],
       [0.76400887, 0.64126327],
       [0.20350213, 0.4635834 ],
       [0.86582915, 0.20263217],
       [0.42274996, 0.67091027],
       [0.75127929, 0.01813313],
       [0.81732532, 0.40918105],
       [0.08500303, 0.0341819 ],
       [0.78106711, 0.69666425],
       [0.92082179, 0.53160548]])

da.coords

Coordinates:
    *empty*

da.dims

('dim_0', 'dim_1')

da.attrs

{}

We’ll add coordinates and dimension names and see how indexing works:

dims = ('time', 'repetition')
coords = {'time': np.linspace(0, 1, num=10),
          'repetition': np.arange(2)}
da2 = xr.DataArray(np.random.random((10, 2)), dims=dims, coords=coords)
da2

<xarray.DataArray (time: 10, repetition: 2)> Size: 160B
array([[0.37241498, 0.88240173],
       [0.20473639, 0.65474677],
       [0.81009228, 0.41256622],
       [0.54727226, 0.67432104],
       [0.96431084, 0.09172217],
       [0.58432268, 0.92033857],
       [0.46211278, 0.01081154],
       [0.90861634, 0.91440916],
       [0.27944533, 0.42343804],
       [0.16394021, 0.24650172]])
Coordinates:
  * time        (time) float64 80B 0.0 0.1111 0.2222 ... 0.7778 0.8889 1.0
  * repetition  (repetition) int64 16B 0 1

xarray.DataArray

• time: 10
• repetition: 2

• 0.3724 0.8824 0.2047 0.6547 0.8101 ... 0.2794 0.4234 0.1639 0.2465

  array([[0.37241498, 0.88240173],
         [0.20473639, 0.65474677],
         [0.81009228, 0.41256622],
         [0.54727226, 0.67432104],
         [0.96431084, 0.09172217],
         [0.58432268, 0.92033857],
         [0.46211278, 0.01081154],
         [0.90861634, 0.91440916],
         [0.27944533, 0.42343804],
         [0.16394021, 0.24650172]])

• Coordinates: (2)
  • time
    (time)
    float64
    0.0 0.1111 0.2222 ... 0.8889 1.0

    array([0.      , 0.111111, 0.222222, 0.333333, 0.444444, 0.555556, 0.666667,
           0.777778, 0.888889, 1.      ])

  • repetition
    (repetition)
    int64
    0 1

    array([0, 1])

• Indexes: (2)
  • time
    PandasIndex

    PandasIndex(Index([               0.0, 0.1111111111111111, 0.2222222222222222,
           0.3333333333333333, 0.4444444444444444, 0.5555555555555556,
           0.6666666666666666, 0.7777777777777777, 0.8888888888888888,
                          1.0],
          dtype='float64', name='time'))

  • repetition
    PandasIndex

    PandasIndex(Index([0, 1], dtype='int64', name='repetition'))

• Attributes: (0)

da2.loc[0.1:0.3, 1]  # rows 1-2 in the second column

<xarray.DataArray (time: 2)> Size: 16B
array([0.65474677, 0.41256622])
Coordinates:
  * time        (time) float64 16B 0.1111 0.2222
    repetition  int64 8B 1

xarray.DataArray

• time: 2

• 0.6547 0.4126

  array([0.65474677, 0.41256622])

• Coordinates: (2)
  • time
    (time)
    float64
    0.1111 0.2222

    array([0.111111, 0.222222])

  • repetition
    ()
    int64
    1

    array(1)

• Indexes: (1)
  • time
    PandasIndex

    PandasIndex(Index([0.1111111111111111, 0.2222222222222222], dtype='float64', name='time'))

• Attributes: (0)

da2.isel(time=slice(3, 7))  # dimension name and integer label (sel = select)

<xarray.DataArray (time: 4, repetition: 2)> Size: 64B
array([[0.54727226, 0.67432104],
       [0.96431084, 0.09172217],
       [0.58432268, 0.92033857],
       [0.46211278, 0.01081154]])
Coordinates:
  * time        (time) float64 32B 0.3333 0.4444 0.5556 0.6667
  * repetition  (repetition) int64 16B 0 1

xarray.DataArray

• time: 4
• repetition: 2

• 0.5473 0.6743 0.9643 0.09172 0.5843 0.9203 0.4621 0.01081

  array([[0.54727226, 0.67432104],
         [0.96431084, 0.09172217],
         [0.58432268, 0.92033857],
         [0.46211278, 0.01081154]])

• Coordinates: (2)
  • time
    (time)
    float64
    0.3333 0.4444 0.5556 0.6667

    array([0.333333, 0.444444, 0.555556, 0.666667])

  • repetition
    (repetition)
    int64
    0 1

    array([0, 1])

• Indexes: (2)
  • time
    PandasIndex

    PandasIndex(Index([0.3333333333333333, 0.4444444444444444, 0.5555555555555556,
           0.6666666666666666],
          dtype='float64', name='time'))

  • repetition
    PandasIndex

    PandasIndex(Index([0, 1], dtype='int64', name='repetition'))

• Attributes: (0)

da2.sel(time=slice(0.1, 0.3), repetition=[1])  # dimension name and coordinate label

<xarray.DataArray (time: 2, repetition: 1)> Size: 16B
array([[0.65474677],
       [0.41256622]])
Coordinates:
  * time        (time) float64 16B 0.1111 0.2222
  * repetition  (repetition) int64 8B 1

xarray.DataArray

• time: 2
• repetition: 1

• 0.6547 0.4126

  array([[0.65474677],
         [0.41256622]])

• Coordinates: (2)
  • time
    (time)
    float64
    0.1111 0.2222

    array([0.111111, 0.222222])

  • repetition
    (repetition)
    int64
    1

    array([1])

• Indexes: (2)
  • time
    PandasIndex

    PandasIndex(Index([0.1111111111111111, 0.2222222222222222], dtype='float64', name='time'))

  • repetition
    PandasIndex

    PandasIndex(Index([1], dtype='int64', name='repetition'))

• Attributes: (0)

Other operations on DataArray instances, such as computations, grouping and such, are done very similarly to dataframes and numpy arrays.

Dataset

A Dataset is to a DataArray what a DataFrame is to a Series. In other words, it’s a collection of DataArray instances that share coordinates.

da2  # a reminder. We notice that this could've been a DataFrame as well

<xarray.DataArray (time: 10, repetition: 2)> Size: 160B
array([[0.37241498, 0.88240173],
       [0.20473639, 0.65474677],
       [0.81009228, 0.41256622],
       [0.54727226, 0.67432104],
       [0.96431084, 0.09172217],
       [0.58432268, 0.92033857],
       [0.46211278, 0.01081154],
       [0.90861634, 0.91440916],
       [0.27944533, 0.42343804],
       [0.16394021, 0.24650172]])
Coordinates:
  * time        (time) float64 80B 0.0 0.1111 0.2222 ... 0.7778 0.8889 1.0
  * repetition  (repetition) int64 16B 0 1

xarray.DataArray

• time: 10
• repetition: 2

• 0.3724 0.8824 0.2047 0.6547 0.8101 ... 0.2794 0.4234 0.1639 0.2465

  array([[0.37241498, 0.88240173],
         [0.20473639, 0.65474677],
         [0.81009228, 0.41256622],
         [0.54727226, 0.67432104],
         [0.96431084, 0.09172217],
         [0.58432268, 0.92033857],
         [0.46211278, 0.01081154],
         [0.90861634, 0.91440916],
         [0.27944533, 0.42343804],
         [0.16394021, 0.24650172]])

• Coordinates: (2)
  • time
    (time)
    float64
    0.0 0.1111 0.2222 ... 0.8889 1.0

    array([0.      , 0.111111, 0.222222, 0.333333, 0.444444, 0.555556, 0.666667,
           0.777778, 0.888889, 1.      ])

  • repetition
    (repetition)
    int64
    0 1

    array([0, 1])

• Indexes: (2)
  • time
    PandasIndex

    PandasIndex(Index([               0.0, 0.1111111111111111, 0.2222222222222222,
           0.3333333333333333, 0.4444444444444444, 0.5555555555555556,
           0.6666666666666666, 0.7777777777777777, 0.8888888888888888,
                          1.0],
          dtype='float64', name='time'))

  • repetition
    PandasIndex

    PandasIndex(Index([0, 1], dtype='int64', name='repetition'))

• Attributes: (0)

ds = xr.Dataset({'ephys': da2,
                 'calcium': ('time', np.random.random(10))},
                attrs={'AnimalD': 701,
                       'ExperimentType': 'double',
                       'Sex': 'Male'})
ds

<xarray.Dataset> Size: 336B
Dimensions:     (time: 10, repetition: 2)
Coordinates:
  * time        (time) float64 80B 0.0 0.1111 0.2222 ... 0.7778 0.8889 1.0
  * repetition  (repetition) int64 16B 0 1
Data variables:
    ephys       (time, repetition) float64 160B 0.3724 0.8824 ... 0.1639 0.2465
    calcium     (time) float64 80B 0.5487 0.6746 0.9419 ... 0.4587 0.2005 0.9001
Attributes:
    AnimalD:         701
    ExperimentType:  double
    Sex:             Male

xarray.Dataset

• Dimensions:
  • time: 10
  • repetition: 2
• Coordinates: (2)
  • time
    (time)
    float64
    0.0 0.1111 0.2222 ... 0.8889 1.0

    array([0.      , 0.111111, 0.222222, 0.333333, 0.444444, 0.555556, 0.666667,
           0.777778, 0.888889, 1.      ])

  • repetition
    (repetition)
    int64
    0 1

    array([0, 1])

• Data variables: (2)
  • ephys
    (time, repetition)
    float64
    0.3724 0.8824 ... 0.1639 0.2465

    array([[0.37241498, 0.88240173],
           [0.20473639, 0.65474677],
           [0.81009228, 0.41256622],
           [0.54727226, 0.67432104],
           [0.96431084, 0.09172217],
           [0.58432268, 0.92033857],
           [0.46211278, 0.01081154],
           [0.90861634, 0.91440916],
           [0.27944533, 0.42343804],
           [0.16394021, 0.24650172]])

  • calcium
    (time)
    float64
    0.5487 0.6746 ... 0.2005 0.9001

    array([0.54869844, 0.67462358, 0.94187829, 0.50491475, 0.61722708,
           0.02759511, 0.03301107, 0.45867716, 0.20045455, 0.90006834])

• Indexes: (2)
  • time
    PandasIndex

    PandasIndex(Index([               0.0, 0.1111111111111111, 0.2222222222222222,
           0.3333333333333333, 0.4444444444444444, 0.5555555555555556,
           0.6666666666666666, 0.7777777777777777, 0.8888888888888888,
                          1.0],
          dtype='float64', name='time'))

  • repetition
    PandasIndex

    PandasIndex(Index([0, 1], dtype='int64', name='repetition'))

• Attributes: (3)

  AnimalD :

  701

  ExperimentType :

  double

  Sex :

  Male

ds['ephys']  # individual DataArrays can be dissimilar in shape

<xarray.DataArray 'ephys' (time: 10, repetition: 2)> Size: 160B
array([[0.37241498, 0.88240173],
       [0.20473639, 0.65474677],
       [0.81009228, 0.41256622],
       [0.54727226, 0.67432104],
       [0.96431084, 0.09172217],
       [0.58432268, 0.92033857],
       [0.46211278, 0.01081154],
       [0.90861634, 0.91440916],
       [0.27944533, 0.42343804],
       [0.16394021, 0.24650172]])
Coordinates:
  * time        (time) float64 80B 0.0 0.1111 0.2222 ... 0.7778 0.8889 1.0
  * repetition  (repetition) int64 16B 0 1

xarray.DataArray

'ephys'

• time: 10
• repetition: 2

• 0.3724 0.8824 0.2047 0.6547 0.8101 ... 0.2794 0.4234 0.1639 0.2465

  array([[0.37241498, 0.88240173],
         [0.20473639, 0.65474677],
         [0.81009228, 0.41256622],
         [0.54727226, 0.67432104],
         [0.96431084, 0.09172217],
         [0.58432268, 0.92033857],
         [0.46211278, 0.01081154],
         [0.90861634, 0.91440916],
         [0.27944533, 0.42343804],
         [0.16394021, 0.24650172]])

• Coordinates: (2)
  • time
    (time)
    float64
    0.0 0.1111 0.2222 ... 0.8889 1.0

    array([0.      , 0.111111, 0.222222, 0.333333, 0.444444, 0.555556, 0.666667,
           0.777778, 0.888889, 1.      ])

  • repetition
    (repetition)
    int64
    0 1

    array([0, 1])

• Indexes: (2)
  • time
    PandasIndex

    PandasIndex(Index([               0.0, 0.1111111111111111, 0.2222222222222222,
           0.3333333333333333, 0.4444444444444444, 0.5555555555555556,
           0.6666666666666666, 0.7777777777777777, 0.8888888888888888,
                          1.0],
          dtype='float64', name='time'))

  • repetition
    PandasIndex

    PandasIndex(Index([0, 1], dtype='int64', name='repetition'))

• Attributes: (0)

Exercise: Rat Visual Stimulus Experiment Database

You’re measuring the potential of neurons in a rat’s brain over time in response to flashes of light using a multi-electrode array surgically inserted into the rat’s skull. Each trial is two seconds long, and one second into the trial a short, 100 ms, bright light is flashed at the animal. After 30 seconds the experiment is replicated, for a total of 4 repetitions. The relevant parameters are the following:

• Rat ID.

• Experimenter name.

• Rat gender.

• Measured voltage (10 electrode, 10k samples representing two seconds).

• Stimulus index (mark differently the pre-, during- and post-stimulus time).

• Repetition number.

Mock data and model it, you can add more parameters if you feel so.

Experimental timeline:

       1s          100ms             0.9s             30s
Start -----> Flash -----> End flash -----> End trial -----> New trial
|                                                                    |
|--------------------------------------------------------------------|
                                   x4

Methods and functions to implement

1. There should be a class holding this data table, VisualStimData, alongside several methods for the analysis of the data. The class should have a data attribute containing the data table, in a xarray.DataArray or a xarray.Dataset.

2. Write a function (not a method) that returns an instance of the class with mock data.

   def mock_stim_data() -> VisualStimData:
       """ Creates a new VisualStimData instance with mock data """
   

   When simulating the recorded voltage, it’s completely fine to not model spikes precisely, with leaky integration and so forth - randoming numbers and treating them as the recorded neural potential is fine. There are quite a few ways to model real neurons, if so you wish, brian being one of them. If your own research will benefit from knowing how to use these tools, this exercise is a great place to start familiarizing yourself with them.

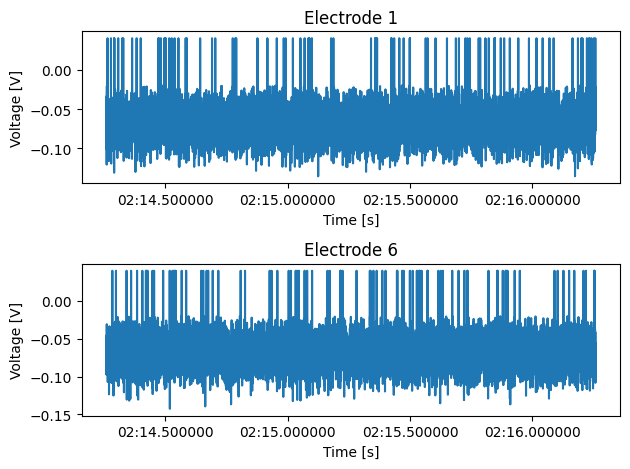
3. Write a method that receives a repetition number, rat ID, and a list of electrode numbers, and plots the voltage recorded from these electrodes. The single figure should be divided into however many plots needed, depending on the length of the list of electrode numbers.

   def plot_electrode(self, rep_number: int, rat_id: int, elec_number: tuple=(0,)):
       """
       Plots the voltage of the electrodes in "elec_number" for the rat "rat_id" in the repetition
       "rep_number". Shows a single figure with subplots.
       """
   

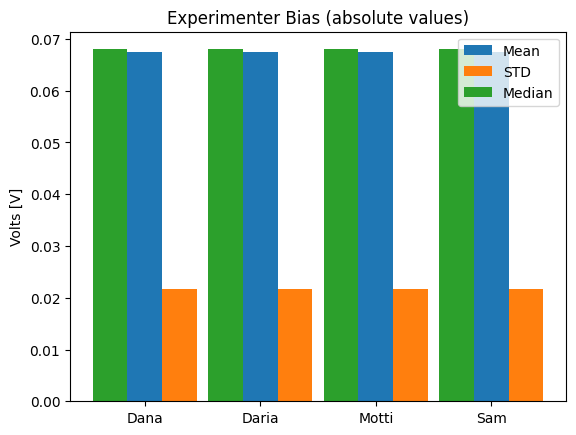
4. To see if the different experimenters influence the measurements, write a method that calculates the mean, standard deviation and median of the average voltage trace across all repetitions, for each experimenter, and shows a bar plot of it.

   def experimenter_bias(self):
       """ Shows the statistics of the average recording across all experimenters """
   

Exercise solutions below…

Show code cell source Hide code cell source

import xarray as xr
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt


class VisualStimData:
    """
    Data and methods for the visual stimulus ePhys experiment.
    The data table itself is held in self.data, an `xarray` object.
    Inputs:
        data: xr.DataArray or xr.Dataset
    Methods:
         ...
    """
    def __init__(self, data: xr.Dataset, ):
        assert isinstance(data, xr.Dataset)
        self.data = data


    def plot_electrode(self, rep_number: int, rat_id: int, elec_number: tuple=(0,)):
        """
        Plots the voltage of the electrodes in "elec_number" for the rat "rat_id" in the repetition
        "rep_number". Shows a single figure with two subplots, for male and female rats.
        """
        fig, axes = plt.subplots(len(elec_number), 1)
        axes = np.array([axes]) if isinstance(axes, plt.Axes) else axes
        time = self.data['time']
        for ax, elec in zip(axes, elec_number):
            to_plot = self.data.sel(rep=rep_number, rat_id=rat_id, elec=elec)['volt'].values
            ax.plot(time, to_plot)
            ax.set_xlabel('Time [s]')
            ax.set_ylabel('Voltage [V]')
            ax.set_title(f'Electrode {elec}')

        fig.tight_layout()

    def experimenter_bias(self):
        """ Shows the statistics of the average recording across all experimenters """
        names = np.unique(self.data.coords['exp_name'].values)
        means = []
        stds = []
        medians = []
        for experimenter in names:
            data = self.data.sel(exp_name=experimenter)['volt'].values
            means.append(np.abs(data.mean()))
            stds.append(np.abs(data.std()))
            medians.append(np.abs(np.median(data)))

        # Plotting
        fig, ax = plt.subplots()
        x_locs = np.arange(len(names))
        width = 0.3
        rect0 = ax.bar(x_locs, means, width, color='C0')
        rect1 = ax.bar(x_locs + width, stds, width, color='C1')
        rect2 = ax.bar(x_locs - width, medians, width, color='C2')

        ax.set_xticks(x_locs)
        ax.set_xticklabels(names)
        ax.legend((rect0[0], rect1[0], rect2[0]), ('Mean', 'STD', 'Median'))
        ax.set_title('Experimenter Bias (absolute values)')
        ax.set_ylabel('Volts [V]')

Show code cell source Hide code cell source

def mock_stim_data() -> VisualStimData:
    """ Creates a new VisualStimData instance with mock data """
    num_of_animals = 20
    num_of_reps = 4
    reps = np.arange(num_of_reps, dtype=np.uint8)
    total_num_of_exp = num_of_animals * num_of_reps
    exp_number = np.arange(total_num_of_exp, dtype=np.uint32)
    
    rat_id_ints, rat_id = _generate_rat_data(num_of_animals)
    room_temp, room_humid = _generate_temp_hum_values(total_num_of_exp)
    experimenters = _generate_experimenter_names(num_of_animals, num_of_reps)
    rat_sex = _generate_rat_gender(num_of_animals, num_of_reps)
    stim, electrode_array, time, volt = _generate_voltage_stim(num_of_animals, num_of_reps)

    # Construct the Dataset - this could be done with a pd.MultiIndex as well
    ds = xr.Dataset({'temp': (['num'], room_temp),
                     'humid': (['num'], room_humid),
                     'volt': (['elec', 'time', 'rat_id', 'rep'], volt),
                     'stim': (['time'], stim)},
                    coords={'elec': electrode_array,
                            'time': time,
                            'rat_id': rat_id,
                            'rep': reps,
                            'exp_name': experimenters,
                            'sex': rat_sex,
                            'num': exp_number,
                            })

    ds.attrs['exp_date'] = pd.to_datetime('today')
    ds.attrs['rat_strain'] = 'Sprague Dawley'

    return VisualStimData(ds)
    
def _generate_rat_data(num_of_animals):
    rat_id_ints = np.random.choice(np.arange(100, 900), size=300, replace=False)
    rat_id = np.random.choice(rat_id_ints, size=num_of_animals, replace=False)
    return rat_id_ints, rat_id


def _generate_temp_hum_values(total_num_of_exp):
    room_temp = np.random.random(total_num_of_exp) * 3 + 23  # between 23 and 26 C
    room_humid = np.random.randint(30, 70, size=total_num_of_exp)
    return room_temp, room_humid

def _generate_experimenter_names(num_of_animals, num_of_reps):
    names = ['Dana', 'Motti', 'Sam', 'Daria']
    experimenters = np.random.choice(names, size=num_of_animals, replace=True)
    experimenters = np.tile(experimenters, num_of_reps)
    return experimenters

def _generate_rat_gender(num_of_animals, num_of_reps):
    sex = ['F', 'M']
    rat_sex = np.random.choice(sex, size=num_of_animals, replace=True)
    rat_sex = np.tile(rat_sex, num_of_reps)
    return rat_sex


def _generate_voltage_stim(num_of_animals, num_of_reps):
    pre_stim = 1  # seconds
    stim_time = 0.1  # seconds
    post_stim = 0.9  # seconds
    sampling_rate = 5000  # Hz
    freq = 1 / sampling_rate
    experiment_length = int(pre_stim + stim_time + post_stim)
    electrodes = 10
    samples = sampling_rate * experiment_length

    # Random voltage values from N(0.068, 0.0004)
    volt = 0.02 * np.random.randn(electrodes, samples, num_of_animals,
                                 num_of_reps).astype(np.float32) - 0.068  # in volts, not millivolts
    volt[volt > -0.02] = 0.04  # "spikes"
    time = pd.date_range(start=pd.to_datetime('today'), periods=experiment_length * sampling_rate,
                         freq=f'{freq}S')
    electrode_array = np.arange(electrodes, dtype=np.uint16)

    # Stim index - -1 is pre, 0 is stim, 1 is post
    stim = np.zeros(int(samples), dtype=np.int8)
    stim[:int(pre_stim*sampling_rate)] = -1
    stim[int((pre_stim + stim_time)*sampling_rate):] += 1
    return stim, electrode_array, time, volt

Show code cell source Hide code cell source

# Run the solution
stim_data = mock_stim_data()
ids = stim_data.data['rat_id']
arr = stim_data.plot_electrode(rep_number=2, rat_id=ids[0], elec_number=(1, 6))
stim_data.experimenter_bias()

/tmp/ipykernel_2080/2117857072.py:72: FutureWarning: 'S' is deprecated and will be removed in a future version, please use 's' instead.
  time = pd.date_range(start=pd.to_datetime('today'), periods=experiment_length * sampling_rate,

Show code cell source Hide code cell source

stim_data.data

<xarray.Dataset> Size: 32MB
Dimensions:   (num: 80, elec: 10, time: 10000, rat_id: 20, rep: 4,
               exp_name: 80, sex: 80)
Coordinates:
  * elec      (elec) uint16 20B 0 1 2 3 4 5 6 7 8 9
  * time      (time) datetime64[ns] 80kB 2024-07-18T08:08:24.874088 ... 2024-...
  * rat_id    (rat_id) int64 160B 826 116 194 854 824 ... 332 325 554 564 182
  * rep       (rep) uint8 4B 0 1 2 3
  * exp_name  (exp_name) <U5 2kB 'Motti' 'Dana' 'Daria' ... 'Motti' 'Sam'
  * sex       (sex) <U1 320B 'F' 'M' 'M' 'M' 'F' 'M' ... 'M' 'F' 'F' 'F' 'F' 'F'
  * num       (num) uint32 320B 0 1 2 3 4 5 6 7 8 ... 71 72 73 74 75 76 77 78 79
Data variables:
    temp      (num) float64 640B 25.04 23.55 23.34 24.25 ... 25.5 23.12 25.61
    humid     (num) int64 640B 50 57 53 33 51 47 46 36 ... 50 35 66 54 56 55 61
    volt      (elec, time, rat_id, rep) float32 32MB -0.07042 ... -0.07559
    stim      (time) int8 10kB -1 -1 -1 -1 -1 -1 -1 -1 -1 ... 1 1 1 1 1 1 1 1 1
Attributes:
    exp_date:    2024-07-18 08:08:24.876446
    rat_strain:  Sprague Dawley

xarray.Dataset

• Dimensions:
  • num: 80
  • elec: 10
  • time: 10000
  • rat_id: 20
  • rep: 4
  • exp_name: 80
  • sex: 80
• Coordinates: (7)
  • elec
    (elec)
    uint16
    0 1 2 3 4 5 6 7 8 9

    array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9], dtype=uint16)

  • time
    (time)
    datetime64[ns]
    2024-07-18T08:08:24.874088 ... 2...

    array(['2024-07-18T08:08:24.874088000', '2024-07-18T08:08:24.874288000',
           '2024-07-18T08:08:24.874488000', ..., '2024-07-18T08:08:26.873488000',
           '2024-07-18T08:08:26.873688000', '2024-07-18T08:08:26.873888000'],
          dtype='datetime64[ns]')

  • rat_id
    (rat_id)
    int64
    826 116 194 854 ... 325 554 564 182

    array([826, 116, 194, 854, 824, 516, 441, 580, 502, 607, 167, 161, 378, 382,
           489, 332, 325, 554, 564, 182])

  • rep
    (rep)
    uint8
    0 1 2 3

    array([0, 1, 2, 3], dtype=uint8)

  • exp_name
    (exp_name)
    <U5
    'Motti' 'Dana' ... 'Motti' 'Sam'

    array(['Motti', 'Dana', 'Daria', 'Daria', 'Motti', 'Motti', 'Motti', 'Motti',
           'Daria', 'Sam', 'Sam', 'Sam', 'Motti', 'Daria', 'Daria', 'Dana', 'Dana',
           'Daria', 'Motti', 'Sam', 'Motti', 'Dana', 'Daria', 'Daria', 'Motti',
           'Motti', 'Motti', 'Motti', 'Daria', 'Sam', 'Sam', 'Sam', 'Motti',
           'Daria', 'Daria', 'Dana', 'Dana', 'Daria', 'Motti', 'Sam', 'Motti',
           'Dana', 'Daria', 'Daria', 'Motti', 'Motti', 'Motti', 'Motti', 'Daria',
           'Sam', 'Sam', 'Sam', 'Motti', 'Daria', 'Daria', 'Dana', 'Dana', 'Daria',
           'Motti', 'Sam', 'Motti', 'Dana', 'Daria', 'Daria', 'Motti', 'Motti',
           'Motti', 'Motti', 'Daria', 'Sam', 'Sam', 'Sam', 'Motti', 'Daria',
           'Daria', 'Dana', 'Dana', 'Daria', 'Motti', 'Sam'], dtype='<U5')

  • sex
    (sex)
    <U1
    'F' 'M' 'M' 'M' ... 'F' 'F' 'F' 'F'

    array(['F', 'M', 'M', 'M', 'F', 'M', 'F', 'M', 'F', 'M', 'M', 'M', 'F', 'F',
           'M', 'F', 'F', 'F', 'F', 'F', 'F', 'M', 'M', 'M', 'F', 'M', 'F', 'M',
           'F', 'M', 'M', 'M', 'F', 'F', 'M', 'F', 'F', 'F', 'F', 'F', 'F', 'M',
           'M', 'M', 'F', 'M', 'F', 'M', 'F', 'M', 'M', 'M', 'F', 'F', 'M', 'F',
           'F', 'F', 'F', 'F', 'F', 'M', 'M', 'M', 'F', 'M', 'F', 'M', 'F', 'M',
           'M', 'M', 'F', 'F', 'M', 'F', 'F', 'F', 'F', 'F'], dtype='<U1')

  • num
    (num)
    uint32
    0 1 2 3 4 5 6 ... 74 75 76 77 78 79

    array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16, 17,
           18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35,
           36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53,
           54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71,
           72, 73, 74, 75, 76, 77, 78, 79], dtype=uint32)

• Data variables: (4)
  • temp
    (num)
    float64
    25.04 23.55 23.34 ... 23.12 25.61

    array([25.03541835, 23.54831327, 23.34040003, 24.2540961 , 25.28342077,
           24.36726407, 24.69275262, 23.29149029, 23.26363152, 25.7332186 ,
           25.69072237, 25.92905511, 23.87617445, 24.52699299, 24.59677252,
           24.69827327, 24.37754438, 23.09374801, 23.27359081, 25.74818829,
           24.74101148, 25.03461719, 25.20656107, 23.87459565, 25.6573337 ,
           24.18817039, 24.41353502, 25.07247843, 24.14912761, 23.86964531,
           23.84791548, 23.18498648, 25.94257442, 25.90341209, 23.44228522,
           23.91170315, 23.3118263 , 25.67538409, 23.58245362, 25.68741677,
           23.91023612, 23.1199664 , 25.96713501, 24.94634217, 24.56983006,
           24.13803938, 25.2124692 , 23.35209609, 24.69362137, 23.36248651,
           24.38294239, 24.44115784, 25.97528759, 23.64486021, 23.45128855,
           23.3351706 , 23.00027704, 24.28778695, 23.55909617, 23.34702304,
           24.4908507 , 25.91060808, 25.81427513, 23.42954437, 23.07657192,
           25.3748447 , 23.97405079, 25.20599456, 23.48454955, 25.40008527,
           25.21328627, 24.19362644, 25.25312332, 24.76321969, 25.48412752,
           25.40684693, 24.73272723, 25.49585776, 23.12158695, 25.61436841])

  • humid
    (num)
    int64
    50 57 53 33 51 ... 66 54 56 55 61

    array([50, 57, 53, 33, 51, 47, 46, 36, 36, 40, 39, 63, 55, 41, 30, 48, 49,
           69, 33, 60, 51, 62, 55, 66, 36, 61, 40, 49, 39, 55, 33, 60, 58, 61,
           30, 61, 52, 42, 59, 33, 33, 51, 64, 56, 35, 40, 31, 44, 48, 35, 38,
           39, 52, 43, 36, 50, 56, 63, 69, 48, 45, 59, 35, 37, 38, 69, 65, 34,
           38, 33, 35, 47, 51, 50, 35, 66, 54, 56, 55, 61])

  • volt
    (elec, time, rat_id, rep)
    float32
    -0.07042 -0.04793 ... -0.07559

    array([[[[-0.07042491, -0.04793479, -0.08237593, -0.06609692],
             [-0.04450458, -0.03924971, -0.05012111, -0.07300416],
             [-0.09728502, -0.05127218, -0.05422613, -0.10707264],
             ...,
             [-0.0843502 , -0.07908794, -0.03750913, -0.08695686],
             [-0.04651171, -0.0537489 , -0.09972455, -0.0443589 ],
             [-0.06271616, -0.06998398, -0.08971268, -0.07826211]],
    
            [[-0.03694284, -0.05475579, -0.05183732, -0.06563897],
             [-0.04494102, -0.08444302, -0.06240668, -0.11985256],
             [-0.04847327, -0.06214765, -0.02567099, -0.03853001],
             ...,
             [-0.05840871, -0.05029096, -0.07795972, -0.09474111],
             [ 0.04      , -0.05914428, -0.06145973, -0.09152371],
             [-0.03292753, -0.03108087,  0.04      , -0.09426469]],
    
            [[-0.02658094, -0.0599652 , -0.06129411, -0.05563358],
             [-0.11363181, -0.06021527, -0.05975988, -0.09989025],
             [-0.05863956, -0.06495883, -0.05258274, -0.04957338],
             ...,
    ...
             [-0.02074302, -0.10968989, -0.08420812, -0.07790664],
             [-0.06924484, -0.0367228 , -0.03298511, -0.06764841],
             [-0.08224092, -0.06420736, -0.07480738, -0.05730415]],
    
            [[-0.05445433, -0.07086552, -0.08033676, -0.05480327],
             [-0.10438563, -0.07364017, -0.06719579, -0.0776565 ],
             [-0.08619005, -0.06734988, -0.0728967 , -0.05651464],
             ...,
             [-0.05424103, -0.07060072, -0.04592092, -0.08452158],
             [-0.08394591,  0.04      , -0.05773523, -0.04325661],
             [-0.05895172, -0.0678663 , -0.09055397, -0.08651623]],
    
            [[-0.04514627, -0.08343941, -0.038571  , -0.0807563 ],
             [-0.05801805, -0.10458787, -0.07679483, -0.04975555],
             [-0.08222186, -0.05961371, -0.08873791, -0.07194869],
             ...,
             [-0.02509183, -0.04726138, -0.07352538, -0.06595003],
             [-0.09070557, -0.04178274, -0.10509336, -0.06146792],
             [-0.06852736, -0.08221334, -0.09439557, -0.07558952]]]],
          dtype=float32)

  • stim
    (time)
    int8
    -1 -1 -1 -1 -1 -1 ... 1 1 1 1 1 1

    array([-1, -1, -1, ...,  1,  1,  1], dtype=int8)

• Indexes: (7)
  • elec
    PandasIndex

    PandasIndex(Index([0, 1, 2, 3, 4, 5, 6, 7, 8, 9], dtype='uint16', name='elec'))

  • time
    PandasIndex

    PandasIndex(DatetimeIndex(['2024-07-18 08:08:24.874088', '2024-07-18 08:08:24.874288',
                   '2024-07-18 08:08:24.874488', '2024-07-18 08:08:24.874688',
                   '2024-07-18 08:08:24.874888', '2024-07-18 08:08:24.875088',
                   '2024-07-18 08:08:24.875288', '2024-07-18 08:08:24.875488',
                   '2024-07-18 08:08:24.875688', '2024-07-18 08:08:24.875888',
                   ...
                   '2024-07-18 08:08:26.872088', '2024-07-18 08:08:26.872288',
                   '2024-07-18 08:08:26.872488', '2024-07-18 08:08:26.872688',
                   '2024-07-18 08:08:26.872888', '2024-07-18 08:08:26.873088',
                   '2024-07-18 08:08:26.873288', '2024-07-18 08:08:26.873488',
                   '2024-07-18 08:08:26.873688', '2024-07-18 08:08:26.873888'],
                  dtype='datetime64[ns]', name='time', length=10000, freq='200us'))

  • rat_id
    PandasIndex

    PandasIndex(Index([826, 116, 194, 854, 824, 516, 441, 580, 502, 607, 167, 161, 378, 382,
           489, 332, 325, 554, 564, 182],
          dtype='int64', name='rat_id'))

  • rep
    PandasIndex

    PandasIndex(Index([0, 1, 2, 3], dtype='uint8', name='rep'))

  • exp_name
    PandasIndex

    PandasIndex(Index(['Motti', 'Dana', 'Daria', 'Daria', 'Motti', 'Motti', 'Motti', 'Motti',
           'Daria', 'Sam', 'Sam', 'Sam', 'Motti', 'Daria', 'Daria', 'Dana', 'Dana',
           'Daria', 'Motti', 'Sam', 'Motti', 'Dana', 'Daria', 'Daria', 'Motti',
           'Motti', 'Motti', 'Motti', 'Daria', 'Sam', 'Sam', 'Sam', 'Motti',
           'Daria', 'Daria', 'Dana', 'Dana', 'Daria', 'Motti', 'Sam', 'Motti',
           'Dana', 'Daria', 'Daria', 'Motti', 'Motti', 'Motti', 'Motti', 'Daria',
           'Sam', 'Sam', 'Sam', 'Motti', 'Daria', 'Daria', 'Dana', 'Dana', 'Daria',
           'Motti', 'Sam', 'Motti', 'Dana', 'Daria', 'Daria', 'Motti', 'Motti',
           'Motti', 'Motti', 'Daria', 'Sam', 'Sam', 'Sam', 'Motti', 'Daria',
           'Daria', 'Dana', 'Dana', 'Daria', 'Motti', 'Sam'],
          dtype='object', name='exp_name'))

  • sex
    PandasIndex

    PandasIndex(Index(['F', 'M', 'M', 'M', 'F', 'M', 'F', 'M', 'F', 'M', 'M', 'M', 'F', 'F',
           'M', 'F', 'F', 'F', 'F', 'F', 'F', 'M', 'M', 'M', 'F', 'M', 'F', 'M',
           'F', 'M', 'M', 'M', 'F', 'F', 'M', 'F', 'F', 'F', 'F', 'F', 'F', 'M',
           'M', 'M', 'F', 'M', 'F', 'M', 'F', 'M', 'M', 'M', 'F', 'F', 'M', 'F',
           'F', 'F', 'F', 'F', 'F', 'M', 'M', 'M', 'F', 'M', 'F', 'M', 'F', 'M',
           'M', 'M', 'F', 'F', 'M', 'F', 'F', 'F', 'F', 'F'],
          dtype='object', name='sex'))

  • num
    PandasIndex

    PandasIndex(Index([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16, 17,
           18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35,
           36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53,
           54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71,
           72, 73, 74, 75, 76, 77, 78, 79],
          dtype='uint32', name='num'))

• Attributes: (2)

  exp_date :

  2024-07-18 08:08:24.876446

  rat_strain :

  Sprague Dawley